Presence detection (sparse)

This is a presence detection algorithm built on top of the Sparse service – based on measuring changes in the radar response over time. The algorithm has two main parts which are weighed together:

Inter-frame deviation – detecting (slower) movements between frames

For every frame and depth, we take the mean sweep and feed it through a fast and a slow low pass filter. The inter-frame deviation is based on the deviation between the two filters.

Intra-frame deviation – detecting (faster) movements inside frames

For every frame and depth, the intra-frame deviation is based on the deviation from the mean of the sweeps.

Both the inter- and the intra-frame deviations are filtered both in time and depth. Also, to be more robust against changing environments and variations between sensors, a normalization is done against the noise floor. Finally, some simple processing is applied to generate the final output.

Plots

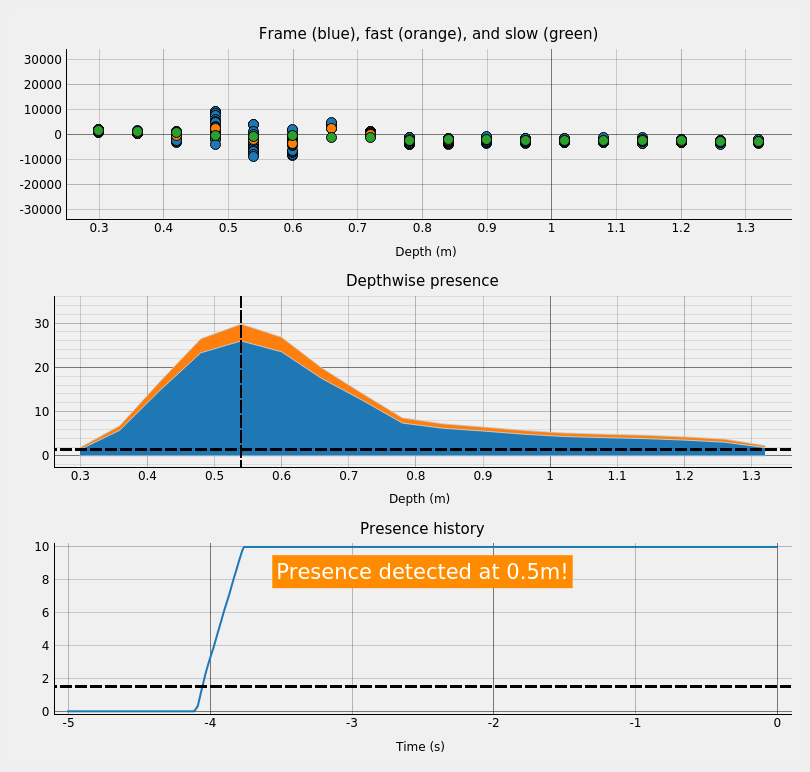
Figure 53 A screenshot of the plots. In it, we can see a target detected at around 0.5 m.

Top plot: The frame \(x\) (blue) along with the fast (orange) and slow (green) filtered mean sweep \(\bar{y}_\text{fast}\) and \(\bar{y}_\text{slow}\) respectively. The distance between the fast (orange) and slow (green) dots is the basis of the inter-frame part, and the spread of the sweeps (blue) is the basis of the intra-frame part.

Middle plot: The “depthwise presence” \(z\). This signal is the time filtered, depth filtered, and normalized version of the weighted sum of the inter- and intra-frame parts. The blue and orange parts show the inter- and intra-frame contributions respectively.

Bottom plot: The detector output \(\bar{v}\). This is obtained from taking the maximum in the above plot and low pass filtering it. The plot is limited to give a clearer view.

Not shown: The noise estimation \(\bar{n}\), used for normalization of the signal.

How to use

Tuning the detector parameters

As previously mentioned, the inter-frame part is good at detecting slower movements, and the intra-frame part is good at detecting faster movements. By slower movements we mean, for example, a person sitting in a chair or sofa. Faster movements could be a person walking or waving their hand.

By default, the detector is configured such that both faster and slower movements are detected. This means that both the inter- and intra-frame parts are used. We recommend this as a starting point.

Tip

The overall sensitivity can be adjusted with the detection_threshold parameter. If the detection toggles too often, try increasing the output_time_const parameter. If it is too sluggish, try decreasing it instead. The effects of these two parameters can be clearly seen in the bottom plot (detector output).

The other parameters are best described by example:

Fast motions - looking for a person walking towards or away from the sensor

Disable the inter-frame part by setting the intra_frame_weight to 1.

The intra-frame part has one parameter - its filter time constant intra_frame_time_const. Look at the depthwise presence (middle plot). If it can’t keep up with the movements, try decreasing the time constant. Instead, if it’s too flickery, try increasing the time constant. This will also be seen in the presence distance.

Since the inter-frame part is disabled, inter-frame parameters have no effect.

Slow motions - looking for a person resting in a sofa

Disable the intra-frame part by setting the intra_frame_weight to 0.

The inter-frame part has a couple of parameters:

inter_frame_fast_cutoff

If too low, some (too fast) motions might not be detected. If too high, unnecessary noise might be entered into the detector.

Values larger than half the update_rate disables this filter. If that is not enough, you need a higher update_rate or to use the intra-frame part.

inter_frame_slow_cutoff

If too high, some (too slow) motions might not be detected. If too low, unnecessary noise might be entered into the detector, and changes to the static environment takes a long time to adjust to.

inter_frame_deviation_time_const

This behaves in the same way as the intra-frame time constant intra_frame_time_const.

Look at the depthwise presence (middle plot). If it can’t keep up with movements changing depth, try decreasing the time constant. Instead, if it’s too flickery, try increasing the time constant.

Since the intra-frame part is disabled, the intra_frame_time_const has no effect.

PCA based noise reduction

Strong static reflectors, such as concrete floor and metal objects, in the FoV of the radar can give higher detection level than the standard noise floor. This can cause false presence detection. Principal component analysis(PCA) based noise reduction suppress detection from static objects while signals from real movements are preserved.

For maximum noise reduction the num_removed_pc is set to 2. If the parameter is set to 0, no PCA based noise reduction is performed. With no strong reflective static objects in the FoV of the radar, PCA based noise reduction can give a minor degradation in performance. In these situations we recommend setting num_removed_pc to 0.

Tuning the service parameters

Always start by setting the range_interval to the desired interval. This is important, since other parameters depend on this.

The update_rate should high enough to keep up with faster motions. However, doing so will increase the duty cycle and therefore the power consumption of the system.

The sweeps_per_frame should also in most cases be set as high as possible, but after the frame rate is set. This will also increase the duty cycle and power consumption of the system.

If you want to distinguish depths with presence from those with no presence, set the sampling_mode to A, otherwise keep it at B (the default) for maximum SNR.

Limiting the sweep_rate or decreasing hw_accelerated_average_samples is not recommend.

Detailed description

The Sparse service returns data frames in the form of \(N_s\) sweeps, each consisting of \(N_d\) range depth points, normally spaced roughly 6 cm apart. We denote frames captured using the sparse service as \(x(f,s,d)\), where \(f\) denotes the frame index, \(s\) the sweep index and \(d\) the range depth index. As described in the documentation of the Sparse service, small movements within the field of view of the radar appear as sinusoidal movements of the sampling points over time. Thus, for each range depth point, we wish to detect changes between individual point samples occurring in the \(f\) and \(s\) dimensions.

Inter-frame detection basis

In the typical case, the time between frames is far greater than the time between sweeps. Typically, the frame rate is 2 - 100 Hz while the sweep rate is 3 - 30 kHz. Therefore, when looking for slow movements – presence – the sweeps in a frame can be regarded as being sampled at the same point in time. This allows us to take the mean over all sweeps in a frame without losing any information. Let the mean sweep be denoted as

\[y(f, d) = \frac{1}{N_s} \sum_s x(f, s, d)\]

We take this mean sweep \(y\) and depthwise run it though two exponential smoothing filters (first order IIR low pass filters). One slower filter with a larger smoothing factor, and one faster filter with a smaller smoothing factor. Let \(\alpha_\text{fast}\) and \(\alpha_\text{slow}\) be the smoothing factors and \(\bar{y}_\text{fast}\) and \(\bar{y}_\text{slow}\) be the filtered sweep means. For every depth \(d\) in every new frame \(f\):

\[ \begin{align}\begin{aligned}\bar{y}_\text{slow}(f, d) = \alpha_\text{slow} \cdot \bar{y}_\text{slow}(f-1, d) + (1 - \alpha_\text{slow}) \cdot y(f, d)\\\bar{y}_\text{fast}(f, d) = \alpha_\text{fast} \cdot \bar{y}_\text{fast}(f-1, d) + (1 - \alpha_\text{fast}) \cdot y(f, d)\end{aligned}\end{align} \]

Note

The smoothing factors \(\alpha_\text{fast}\) and \(\alpha_\text{slow}\) are set through the inter_frame_fast_cutoff and inter_frame_slow_cutoff parameters. The relationship between cutoff frequency and smoothing factor is described under Calculating smoothing factors.

From the fast and slow filtered sweep means, a deviation metric \(s_\text{inter}\) is obtained by taking the absolute deviation between the two:

\[s_\text{inter}(f, d) = \sqrt{N_s} \cdot |\bar{y}_\text{fast}(f, d) - \bar{y}_\text{slow}(f, d)|\]

Where \(\sqrt{N_s}\) is a normalization constant. In other words, \(s_\text{inter}\) relates to the instantaneous power of a bandpass filtered version of \(y\). This metric is then filtered again with a smoothing factor, \(\alpha_\text{dev}\), set through the inter_frame_deviation_time_const parameter, to get a more stable metric:

\[\bar{s}_\text{inter}(f, d) = \alpha_\text{dev} \cdot \bar{s}_\text{inter}(f-1, d) + (1 - \alpha_\text{dev}) \cdot s_\text{inter}(f, d)\]

This is the basis of the inter-frame presence detection. In a few words - depthwise low pass filtered power of the bandpass filtered signal. But before it’s used, it’s favorable to normalize it with noise floor, discussed in later sections.

Intra-frame detection basis

There are cases where the motion is too fast for the inter-frame to pick up. Often, we are interested in seeing such movements as well, and this is what the intra-frame part is for. The idea is simple – for every frame we depthwise take the deviation from the sweep mean and low pass (smoothing) filter it.

Let the deviation from the be mean be:

\[s_\text{intra}(f, d) = \sqrt{\frac{N_s}{N_s - 1}} \cdot \frac{1}{N_s} \sum_s |x(f, s, d) - y(f, d)|\]

where the first factor is a correction for the limited number of samples (sweeps).

Then, let the low pass filtered (smoothed) version be:

\[\bar{s}_\text{intra}(f, d) = \alpha_\text{intra} \cdot \bar{s}_\text{intra}(f-1, d) + (1 - \alpha_\text{intra}) \cdot s_\text{intra}(f, d)\]

The smoothing factor \(\alpha_\text{intra}\) is set through the intra_frame_time_const parameter.

Noise estimation

To normalize detection levels, we need an estimate of the noise power generated by the sensor. We assume that from a static channel, i.e., a radar signal with no moving reflections, the noise is white and its power is its variance. However, we do not want to rely on having such a measurement to obtain this estimate.

Since we’re looking for motions generated by humans and other living things, we know that we typically won’t see fast moving objects in the data. In other words, we may assume that high frequency content in the data originates from sensor noise. Since we have a relatively high sweep rate, we may take advantage of this to measure high frequency content.

Extracting the high frequency content from the data can be done in numerous ways. The simplest to implement is possibly a FFT, but it is computationally expensive. Instead, we use another technique which is both robust and cheap.

First, to remove any trends from fast motion in the frame, we differentiate over the sweeps \(N_\text{diff}=3\) times:

\[x'(f, s, d) = x^{(1)}(f, s, d) = x(f, s, d) - x(f, s - 1, d)\]

\[...\]

\[x^{(N_\text{diff})}(f, s, d) = x^{(N_\text{diff} - 1)}(f, s, d) - x^{(N_\text{diff} - 1)}(f, s - 1, d)\]

Then, take the mean absolute deviation:

\[\hat{n}(f, d) = \frac{1}{N_s - N_\text{diff}} \sum_{s=1 + N_\text{diff}}^{N_s} | x^{(N_\text{diff})}(f, s, d) |\]

And normalize such that the expectation value would be the same as if no differentiation was applied:

\[n(f, d) = \hat{n}(f, d) \cdot \left[ \sum_{k=0}^{N_\text{diff}} \binom{N_\text{diff}}{k}^2 \right]^{-1/2}\]

Finally, apply an exponential smoothing filter with a smoothing factor \(\alpha_\text{noise}\) to get a more stable metric:

\[\bar{n}(f, d) = \alpha_\text{noise} \cdot \bar{n}(f-1, d) + (1 - \alpha_\text{noise}) \cdot n(f, d)\]

This smoothing factor is set from a fixed time constant of 1 s.

PCA based noise reduction

Approximate leading principal components are tracked from the noise differentiation. Contributions within the vector space spanned by the tracked vectors are subtracted from the inter-frame and intra-frame deviations used to calculate the inter-frame and intra-frame low pass filtered absolute deviations. With every new frame the principal components are updated by an incremental PCA algorithm, based on the extended approach of Oja’s algorithm in The Fast Convergence of Incremental PCA by Balsubramani et al., 2013.

Generating the detector output

We now have three signals – the inter-frame deviation \(\bar{s}_\text{inter}(f, d)\), the intra-frame deviation \(\bar{s}_\text{intra}(f, d)\), and the noise estimation \(\bar{n}(f, d)\). To form the depthwise output we weigh the inter and intra parts together and normalize with the noise estimation:

\[\bar{s}_n(f, d) = \frac{ w_\text{inter} \cdot \bar{s}_\text{inter}(f, d) + w_\text{intra} \cdot \bar{s}_\text{intra}(f, d) }{ \bar{n}(f, d) }\]

The intra-frame weight \(w_\text{intra}\) is settable through the intra_frame_weight parameter. The inter-frame weight \(w_\text{inter} = 1 - w_\text{intra}\).

Finally, since the reflection typically span several depth points, we apply a small depth filter:

\[z(f, d) = \frac{1}{3} \sum_{i=-1}^{1} \bar{s}_n(f, d + i)\]

where the signal \(\bar{s}_n\) is zero-padded, i.e.:

\[\bar{s}_n(f, d) = 0 \text{ for } d < 1 \text{ and } d > N_d\]

From \(z\), we can extract the information we are looking for. Is there someone present in front of the sensor, and if so, where? To answer this, we simply look for a peak in the data \(z\). To give the detection decision a bit of inertia, we also add a smoothing filter to the peak value.

\[v(f) = \max_d(z(f, d))\]

\[\bar{v}(f) = \alpha_\text{output} \cdot \bar{v}(f-1) + (1 - \alpha_\text{output}) \cdot v(f)\]

\[p = v > v_\text{threshold}\]

\[d_p = \arg\max_d(z(f, d))\]

where \(p\) is the “present”/”not present” output and \(d_p\) is the presence depth index output.

It is possible to tune \(\alpha_\text{output}\) through the output_time_const parameter. The threshold \(v_\text{threshold}\) is settable through the detection_threshold parameter.

Graphical overview

Calculating smoothing factors

Instead of directly setting the smoothing factor of the smoothing filters in the detector, we use cutoff frequencies and time constants. This allows the configuration to be independent of the frame rate.

The symbols used are:

Symbol	Description	Unit
\(\alpha\)	Smoothing factor	1
\(\tau\)	Time constant	s
\(f_c\)	Cutoff frequency	Hz
\(f_f\)	Frame rate	Hz

Going from time constant \(\tau\) to smoothing factor \(\alpha\):

\[\alpha = \exp\left(-\frac{1}{\tau \cdot f_f}\right)\]

The bigger the time constant, the slower the filter.

Going from cutoff frequency \(f_c\) to smoothing factor \(\alpha\):

\[\begin{split}\alpha = \begin{cases} 2 - \cos(2\pi f_c/f_f) - \sqrt{\cos^2(2\pi f_c/f_f) - 4 \cos(2\pi f_c/f_f) + 3} & \text{if } f_c < f_f / 2 \\ 0 & \text{otherwise} \\ \end{cases}\end{split}\]

The lower the cutoff frequency, the slower the filter. The expression is obtained from setting the -3 dB frequency of the resulting exponential filter to be the cutoff frequency. For low cutoff frequencies, the more well known expression \(\alpha = \exp(-2\pi f_c/f_f)\) is a good approximation.

Read more: time constants, cutoff frequencies.

Configuration parameters

class acconeer.exptool.a111.algo.presence_detection_sparse.ProcessingConfiguration

detection_threshold

Level at which the detector output is considered as “present”.

Type: float

Default value: 1.5

inter_frame_fast_cutoff

Cutoff frequency of the low pass filter for the fast filtered sweep mean. No filtering is applied if the cutoff is set over half the frame rate (Nyquist limit).

Type: float

Unit: Hz

Default value: 20.0

inter_frame_slow_cutoff

Cutoff frequency of the low pass filter for the slow filtered sweep mean.

Type: float

Unit: Hz

Default value: 0.2

inter_frame_deviation_time_const

Time constant of the low pass filter for the (inter-frame) deviation between fast and slow.

Type: float

Unit: s

Default value: 0.5

intra_frame_time_const

Time constant for the intra frame part.

Type: float

Unit: s

Default value: 0.15

intra_frame_weight

The weight of the intra-frame part in the final output. A value of 1 corresponds to only using the intra-frame part and a value of 0 corresponds to only using the inter-frame part.

Type: float

Default value: 0.6

output_time_const

Time constant of the low pass filter for the detector output.

Type: float

Unit: s

Default value: 0.5

num_removed_pc

Sets the number of principal components removed in the PCA based noise reduction. Filters out static reflections. Setting to 0 (default) disables the PCA based noise reduction completely.

Type: int

Default value: 0

show_data

Show the plot of the current data frame along with the fast and slow filtered mean sweep (used in the inter-frame part).

Type: bool

Default value: True

show_noise

Show the noise estimation plot.

Type: bool

Default value: False

show_depthwise_output

Show the depthwise presence output plot.

Type: bool

Default value: True

show_sectors

Type: bool

Default value: False

history_plot_ceiling

The highest presence score that will be plotted.

Type: float

Default value: 10.0

history_length_s

Type: float

Unit: s

Default value: 5