Timing

Note

The relationships, equations, and constants described here are approximate, not guaranteed, and may change over RSS releases.

Notation

\(\tau\) - A time duration.

\(f\) - A frequency or rate. Inverse of \(T\).

\(T\) - A period, the time between recurring events. Inverse of \(f\).

\(N\) - A number or amount of something.

Overview

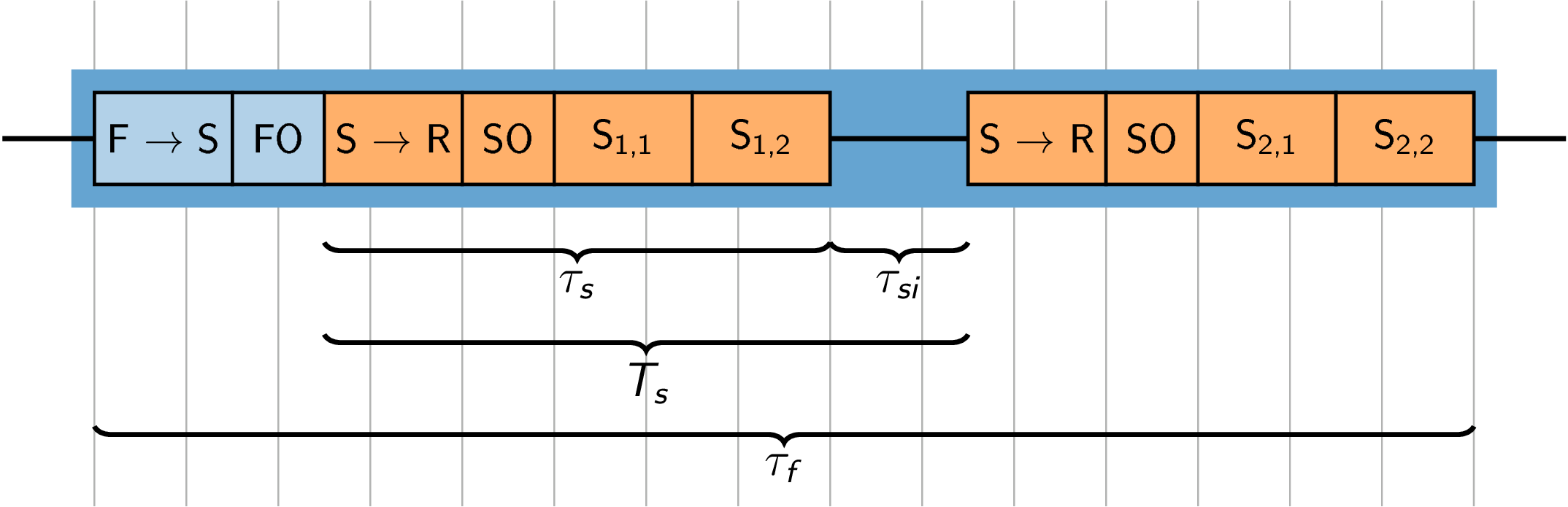
Figure 12 Overview for timing within a frame with two sweeps, in turn consisting of two subsweeps. Not to scale, and subsweeps may have different lengths. F→S and S→R are the times required to transition from the configured inter frame idle state to the inter sweep idle state state, and inter sweep idle state to the ready state, respectively. FO and SO are the fixed overheads on frame and sweep level with duration \(C_f\) and \(C_s\) respectively. \(S_{i,j}\) are subsweeps.

Sample duration

The time to measure a sample \(\tau_\text{sample}\) is the added time per HWAAS for every single measured point. In most cases, this accounts for the largest part of the sensor measurement time. The sample duration \(\tau_\text{sample}\) depends on the configured profile and PRF according to Table 4 below.

Table 4 Approximate sample durations \(\tau_\text{sample}\) for all profile and PRF \(f_p\) combinations.

Profile \ PRF	19.5 MHz	15.6 MHz	13.0 MHz	8.7 MHz	6.5 MHz	5.2 MHz
1	1487 ns	1795 ns	2103 ns	3026 ns	3949 ns	4872 ns
2	N/A	1344 ns	1600 ns	2369 ns	3138 ns	3908 ns
3	N/A	1026 ns	1231 ns	1846 ns	2462 ns	3077 ns
4	N/A	1026 ns	1231 ns	1846 ns	2462 ns	3077 ns
5	N/A	1026 ns	1231 ns	1846 ns	2462 ns	3077 ns

Point duration

The total time it takes to measure a single distance point in a single (sub)sweep is

(6)\[\tau_\text{point} \approx N_a \cdot \tau_\text{sample} + \tau_\text{point overhead}\]

where \(N_a\) is the configured HWAAS (number of averages), and \(\tau_\text{point overhead}\) is given by Table 5 below.

Table 5 Approximate durations of the point overhead \(\tau_\text{point overhead}\) for all profile and PRF \(f_p\) combinations.

Profile \ PRF	19.5 MHz	15.6 MHz	13.0 MHz	8.7 MHz	6.5 MHz	5.2 MHz
1	1744 ns	2102 ns	2462 ns	3539 ns	4615 ns	5692 ns
2	N/A	1612 ns	1920 ns	2844 ns	3766 ns	4689 ns
3	N/A	1282 ns	1539 ns	2308 ns	3077 ns	3846 ns
4	N/A	1282 ns	1539 ns	2308 ns	3077 ns	3846 ns
5	N/A	1282 ns	1539 ns	2308 ns	3077 ns	3846 ns

Subsweep duration

The total time it takes to measure a single subsweep, including the time it takes to initialize the measurement is

(7)\[\tau_\text{subsweep} \approx N_d \cdot \tau_\text{point} + \underbrace{3 \cdot \tau_\text{sample} + C_\text{subsweep}}_\text{overhead}\]

where \(N_d\) is the configured number of distances (num_points), and \(C_\text{subsweep}\) is a fixed overhead, see section Fixed overheads and high speed mode (HSM).

Sweep duration

The time to measure a sweep \(\tau_s\) is the total time it takes to measure a single sweep, including all configured subsweeps and transitioning from the configured inter sweep idle state.

(8)\[\tau_s \approx \tau_{S \rightarrow R} + \sum (\tau_\text{subsweep}) + C_s\]

where \(\tau_{S \rightarrow R}\) is the sweep transition time, and \(C_s\) is a fixed overhead, see section Fixed overheads and high speed mode (HSM).

The sweep transition time \(\tau_{S \rightarrow R}\) is the time required to transition from the configured inter sweep idle state to the ready state. See Table 6 below.

Idle state transition times

Table 6 Approximate transition times between the idle states.

From \ To	Deep sleep	Sleep	Ready
Deep sleep	\(0 \mu\text{s}\)	\(615 \mu\text{s}\)	\(670 \mu\text{s}\)
Sleep	N/A	\(0 \mu\text{s}\)	\(55 \mu\text{s}\)
Ready	N/A	N/A	\(0 \mu\text{s}\)

Sweep period

The sweep period \(T_s\) is the time between the start of two consecutive sweeps in a frame.

If the sweep rate is not set, the sweep period will be equal to the sweep duration; \(T_s = \tau_s\).

If the sweep rate is set, the sensor will idle in the configured inter sweep idle state between sweeps. This idle time is called the inter sweep idle time, \(\tau_{si}\).

(9)\[T_s = \frac{1}{f_s} = \tau_s + \tau_{si}\]

Frame duration

The time to measure a frame \(\tau_f\) is the total time it takes to measure a frame, including all sweeps and transitioning from the configured inter frame idle state.

(10)\[\tau_f \approx \tau_{F \rightarrow S} + (N_s - 1) \cdot T_s + \tau_s + C_f\]

where \(\tau_{F \rightarrow S}\) is the frame transition time, \(N_s\) is the SPF (sweeps per frame), and \(C_f\) is a fixed overhead, see section Fixed overheads and high speed mode (HSM).

The frame transition time \(\tau_{F \rightarrow S}\) is the time required to transition from the configured inter frame idle state to the inter sweep idle state state. See Table 6 above.

Frame period

The frame period \(T_f\) is the time between the start of two consecutive frames. The sensor will idle in the configured inter frame idle state between frames. This idle time is called the inter frame idle time, \(\tau_{fi}\).

(11)\[T_f = \frac{1}{f_f} = \tau_f + \tau_{fi}\]

In most cases, the sensor will not measure (again) until the host commands it to. This means that the frame period, and thus also the inter frame idle time, is given by how the host controls the sensor.

If the frame rate is not set, the sensor will measure immediately once the host commands it to. Thus, the frame period will be larger than the frame duration; \(T_f > \tau_f\).

If the frame rate \(f_f\) is set, the sensor will continue to idle until Eq. 11 is met.

Fixed overheads and high speed mode (HSM)

The fixed overheads for subsweep, \(C_\text{subsweep}\), sweep, \(C_s\), and frame, \(C_f\), are dependent on if high speed mode is activated or not. High speed mode means that the sensor is configured in a way where it can optimize its measurements to obtain as high sweep rate as possible. In order for the sensor to operate in high speed mode, the following configuration constraints apply:

• continuous_sweep_mode: False

• inter_sweep_idle_state: READY

• num_subsweeps: 1

• profile: 3-5

Note that the default RSS Service configuration comply with these constraints which means that high speed mode is activated by default.

The fixed overheads can be seen in Table 7 below.

Table 7 Approximate fixed overhead times.

Mode \ Overhead	\(C_\text{subsweep}\)	\(C_s\)	\(C_f\)
Normal	\(22 \mu\text{s}\)	\(10 \mu\text{s}\)	\(4 \mu\text{s}\)
High speed	\(0 \mu\text{s}\)	\(0 \mu\text{s}\)	\(36 \mu\text{s}\)