Interpreting radar data

The A121 Sparse IQ data is represented by complex numbers, one for each distance sampled. Each number has an amplitude and a phase, the amplitude is obtained by taking the absolute value of the complex number and the phase is obtained by taking the argument of the same complex number. A sweep is a array of these complex values corresponding to an amplitude and phase of the reflected pulses in the configured range.

For any given frame, we let \(z(s, d)\) be the complex IQ value (point) for a sweep \(s\) and a distance point \(d\).

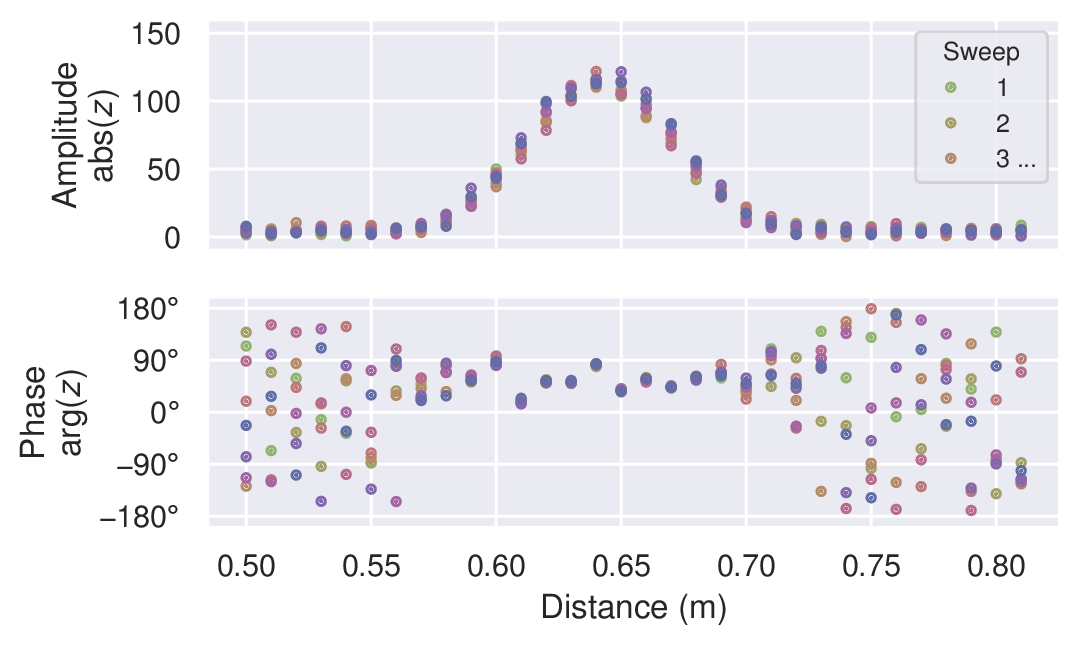
Figure 4 Mocked data of an environment with a single static object.

In the simplest case, we have a static environment in the sensor range. Figure 4 shows an example of this with a single static object at roughly 0.64 m. The sweeps in the frame have similar amplitude and phase, and the variations are due to random errors. As such, they could be coherently averaged together to linearly increase signal-to-noise ratio (SNR). In this context, coherently simply means “in the complex plane”.

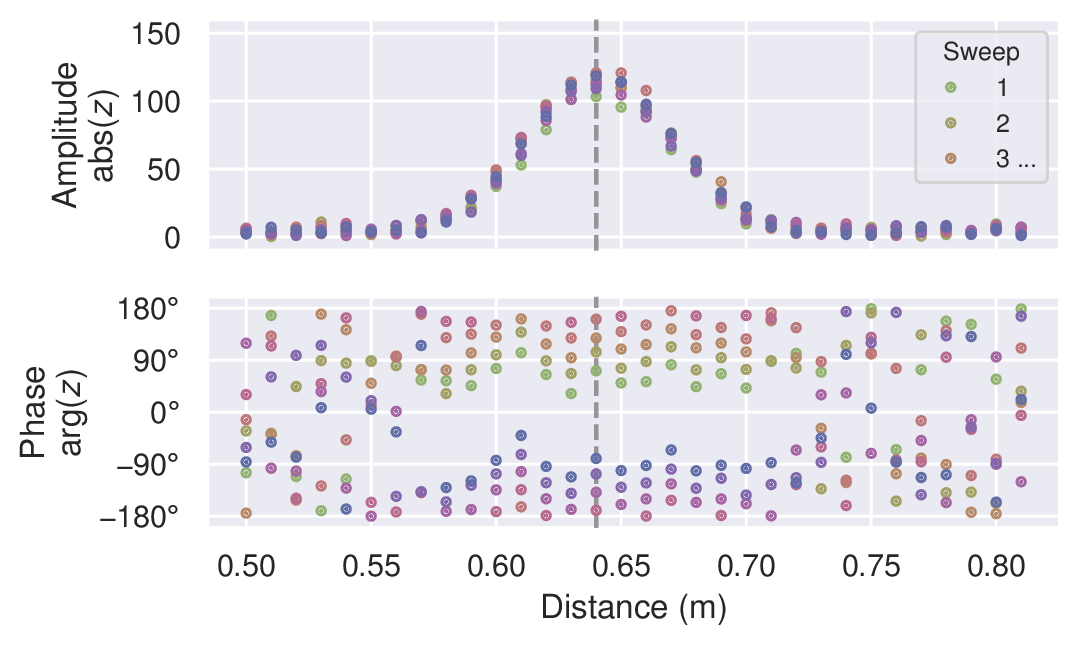
Figure 5 Mocked data of an environment with a single moving object.

In many cases, we want to track and/or detect moving objects in the range. This is demonstrated in Figure 5, where the object has moved during the measurement of the frame. The sweeps still have roughly the same amplitude, but the phase is changing. Due to this, we can no longer coherently average the sweeps together. However, we can still (non-coherently) average the amplitudes.

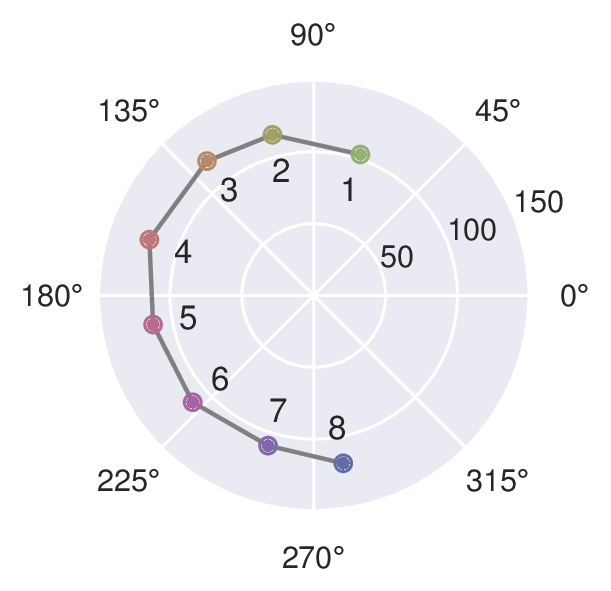
Figure 6 A slice of the mocked data in Figure 5 of an environment with a single moving object, shown in the complex plane.

To track objects over long distances we may track the amplitude peak as it moves, but for accurately measuring finer motions we need to look at the phase. Figure 6 shows the slice of the data along the dashed vertical line in Figure 5. Over the 8 sweeps in the example frame, the phase changed ~ 210°. A full phase rotation of 360° translates to \(\lambda_\text{RF}/2 \approx 2.5 \text{mm}\), so the 210° corresponds to ~ 1.5 mm.

As evident from the example above, even the smallest movements change the phase and thus move the signal in the complex plane. This is utilized in for example the presence detector, which can detect the presence of humans and animals from their breathing motion. It can also be used to detect a change in signal very close to the sensor, creating a “touchless button”.

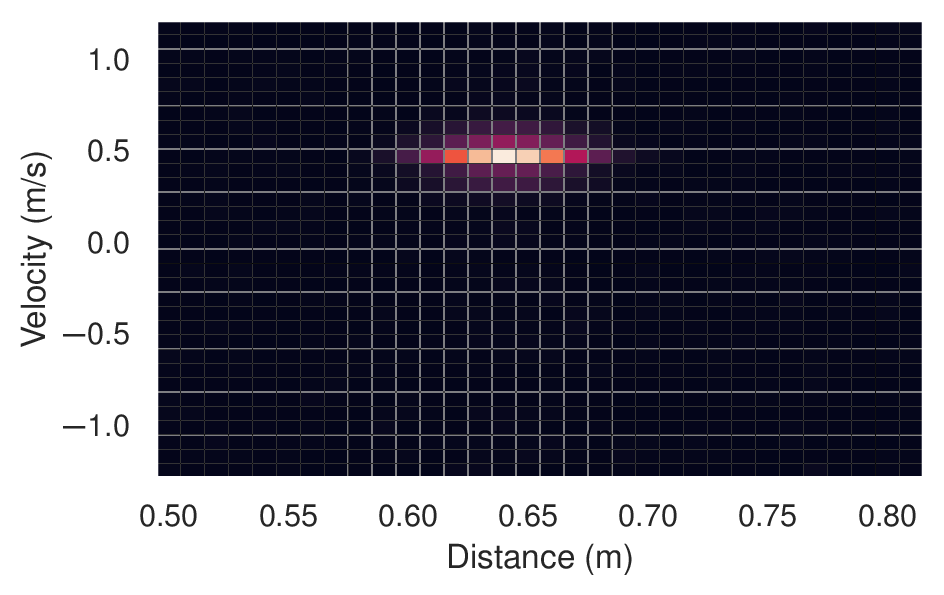
Figure 7 Mocked data of a single moving object, transformed into a distance-velocity (a.k.a. range-Doppler) map.

As shown, the complex data can be used to track the relative movement of an object. By combining this information with the sweep rate, we can also determine its velocity. In practice, this is commonly done by applying the fast Fourier transform (FFT) to the frame over sweeps, giving a distance-velocity (a.k.a.range-Doppler) map. Figure 7 shows an example of this in which we can see an object at ~ 0.64 m with a radial velocity of ~ 0.5 m/s (moving away from the sensor). This method is commonly used for applications such as micro and macro gesture recognition, velocity measurements, and object tracking.